Trending Now
- 1KOSPI
8
- 2Hollywood
8
- 3KOSDAQ
7
- 4shutdown
-2
- 5Bitcoin
-1
- 6ETF
4
- 7Mastercard
3
- 8dollar
2
- 9Ethereum
1
- 10stablecoin

Nous examinons le scénario dans lequel un attaquant tente de générer une chaîne alternative plus rapidement que la chaîne honnête. Même si l’attaquant y parvient, cela n’ouvre pas la voie à des modifications arbitraires, telles que la création de valeur à partir de rien ou l’appropriation de fonds qui ne lui appartiennent pas. Les nœuds du réseau refuseront d’accepter une transaction invalide comme paiement, et les nœuds honnêtes n’accepteront jamais un bloc qui en contient. Un attaquant peut uniquement essayer de modifier l’une de ses propres transactions pour récupérer des fonds qu’il a récemment dépensés.
La course entre la chaîne honnête et la chaîne de l’attaquant peut être modélisée comme une marche aléatoire binomiale. L’événement de succès survient lorsque la chaîne honnête est étendue par un bloc, augmentant ainsi son avance de +1. À l’inverse, un événement d’échec survient lorsque la chaîne de l’attaquant est étendue par un bloc, réduisant l’écart de -1.
La probabilité qu’un attaquant parvienne à rattraper son retard initial est analogue au problème classique de la ruine du joueur. Imaginons un joueur avec un crédit illimité qui démarre avec un déficit et joue un nombre potentiellement infini de parties pour tenter d’atteindre l’équilibre. Nous pouvons alors calculer la probabilité qu’il parvienne à atteindre cet équilibre, ou autrement dit, qu’un attaquant réussisse à rattraper la chaîne honnête, comme suit [8]:
p = probabilité qu’un nœud honnête trouve le prochain bloc q = probabilité que l’attaquant trouve le prochain bloc qz = probabilité que l’attaquant parvienne à rattraper son retard en partant de z blocs derrière
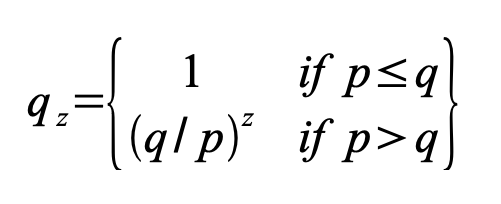
Étant donné notre hypothèse selon laquelle p > q, la probabilité diminue de manière exponentielle à mesure que le nombre de blocs que l’attaquant doit rattraper augmente. Les chances étant contre lui, s’il ne parvient pas à réaliser une avance chanceuse dès le début, ses chances de succès deviennent extrêmement faibles à mesure qu’il prend du retard.
Nous allons maintenant examiner combien de temps le destinataire d’une nouvelle transaction doit attendre pour être suffisamment certain que l’expéditeur ne pourra pas modifier la transaction. Supposons que l’expéditeur soit un attaquant qui veut faire croire au destinataire qu’il a été payé pendant un certain temps, avant d’inverser la transaction pour récupérer les fonds après un délai. Le destinataire sera alerté si cela se produit, mais l’attaquant espère qu’il sera déjà trop tard.
Le destinataire génère une nouvelle paire de clés et transmet la clé publique à l’expéditeur peu de temps avant la signature. Cela empêche l’expéditeur de préparer à l’avance une chaîne de blocs en travaillant dessus continuellement jusqu’à ce qu’il prenne suffisamment d’avance grâce à la chance, puis d’exécuter la transaction à ce moment précis. Une fois la transaction envoyée, l’expéditeur malhonnête commence secrètement à travailler sur une chaîne parallèle contenant une version alternative de cette transaction.
Le destinataire attend que la transaction soit ajoutée à un bloc, puis que z blocs supplémentaires soient liés après celui-ci. Il ne connaît pas précisément l’avancement de l’attaquant, mais si l’on suppose que les blocs honnêtes ont pris le temps moyen prévu par bloc, les progrès potentiels de l’attaquant suivront une distribution de Poisson avec la valeur attendue suivante :
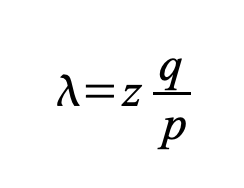
Pour calculer la probabilité que l’attaquant puisse encore rattraper son retard, nous multiplions la densité de la distribution de Poisson pour chaque niveau de progrès qu’il aurait pu réaliser par la probabilité qu’il puisse rattraper à partir de ce point:
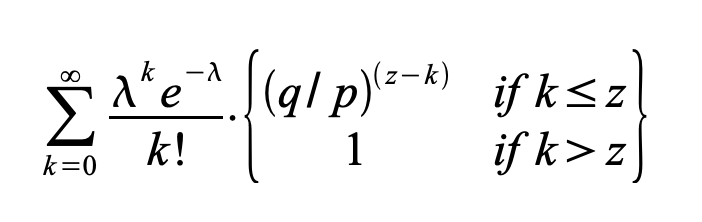
En réorganisant l'équation afin d’éviter de sommer la queue infinie de la distribution…
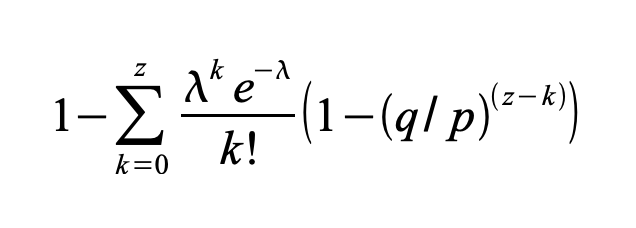
En le convertissant en code C…
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
En exécutant quelques résultats, nous observons que la probabilité diminue de façon exponentielle avec z.
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006
En résolvant pour que P soit inférieur à 0,1%...
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=340